Game Report: Rhythmomachy Basics

Class: Board

Type: Strategy

Number of Players: 2

Reconstructed mainly from primary sources

Date Redacted: March 22, 1998

Redactor: Justin

Sources: Mainly Fulke's The Philosopher's Game.

Reconstruction

Rhythmomachy is, like so many period games, really more a family of games than a single, very specific one. Also called "The Philosopher's Game", it was popular among the intelligentsia for most of period, from the High Middle Ages right through the Renaissance. While never a rival to Chess' popularity, it had a definite niche (as witnessed by its long survival). It is rather unique, being a game mainly of mathematics, combined with more positional strategies like Chess.

Since, as mentioned, there were a number of variants of the game, this article sets out the commonalities. It is not intended to be taken as a full description on its own; rather, it should be considered the common first section of the Rhythmomachy reconstructions I will be writing.

Equipment

The Rhythmomachy board is rectangular, generally 8 squares wide by 16 long. Each player begins with his men arrayed on one of the short ends. In some descriptions, the board is shorter (8 x 14), but the 8 x 16 arrangement seems to be most common. It is unclear to me whether the board was checkered or not; there is no intrinsic reason why it should be, and most of the images don't depict checkering, but a few do. I suspect that both the size and the occasional checkering resulted from the fact that the game is easy to play on two chessboards, set side-by-side; since Chess was quite common in pretty much all cultures that had Rhythmomachy, this was likely a common way to play. Thus, the checkering was probably an accident of that, and the board size standardized on the convenient double-chessboard.

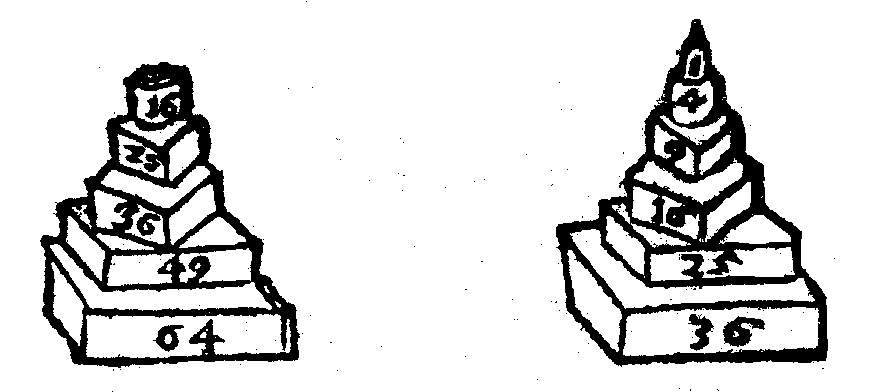
Each player has 24 men, eight round, eight triangular, and eight square. Each man has a number on it; the rationale behind the numbers is discussed below. Rhythmomachy is unusual in that it is an asymmetrical game -- although each player has the same number of pieces, the numbers written on those pieces differ widely. I usually think of one side as "even", and the other "odd", but the reality is more complex than that. The two sides have contrasting colors, usually but not always black and white. I usually play black as odd and white as even out of habit, but that is a semi-arbitrary choice, based on the illustrations in Fulke. On average, the odd numbers are significantly higher than the even numbers. The men are usually flat, and double-sided, with the same number in the opposing color on the opposite side. For my personal sets, I paint the edges of the men with the color of the side they start on, to make them easier to sort for setup.

The Numbers on the Men

The men on each side fall into six "ranks": two ranks of circles, two of triangles, and two of squares. Each rank contains four men on each side. The actual numbers come from straightforward mathematical progressions.

The first rank of rounds can be thought of as the "seeds" for the rest; they are the odd or even numbers less than ten. That is, the evens have 2, 4, 6, and 8; the odds have 3, 5, 7, and 9. Since each rank has four men, each of those flows from a particular seed. (Thus, for the first rank of squares on the even side, one man is based on 2, one on 4, and so on.)

The second rank of rounds are the first rank of rounds squared; thus, on the even side, they are 4, 16, 36, and 64, and on the odd are 9, 25, 49, and 81.

The first rank of triangles are the two rounds added together; thus, on the even side, they are 6 (2 plus 4), 20, 42, and 72, and on the odd are 12, 30, 56, and 90.

The second rank of triangles are the seed plus 1, squared. Thus, on the even side they are 9 (2 plus 1 squared), 25, 49, and 81, and on the odd are 16, 36, 64, and 100.

The first rank of squares are the two triangles added together. Thus, on the even side they are 15 (6 plus 9), 45, 91, and 153, and on the odd are 28, 66, 120, and 190.

The second rank of squares are twice the seed, plus one, squared. Thus, on the even side they are 25 ((2*2)+1, squared), 81, 169, and 289, and on the odd are 49, 121, 225, and 361.

Summarizing all of that into a neat table, we get:

	Evens				Odds
1st Rounds (x)	2	4	6	8	3	5	7	9
2nd Rounds (x²)	4	16	36	64	9	25	49	81
1st Triangles (x + x²)	6	20	42	72	12	30	56	90
2nd Triangles ((x + 1)²)	9	25	49	81	16	36	64	100
1st Squares (x + x² + (x + 1)²)	15	45	91	153	28	66	120	190
2nd Squares ((2x + 1)²)	25	81	169	289	49	121	225	361

The initial arrangement of the men varies from version to version, but typical arrangements can be seen in this Word 97 document and this GIF image (which was taken from Fulke). The ranks on which the men started varied significantly; the layout within those ranks tended to be the same, but there are versions with significantly different layouts.

The Kings

On each side, one square is replaced by a "King" instead. The king is a large number which happens to be a sum of some square numbers, and takes the form of a pyramid of pieces. On the even side, the King is the 91, and is composed of a pyramid of six pieces: a square 36, a square 25, a triangular 16, a triangular 9, a round 4, and a round 1. On the odd side, the King is the 190, and is composed of a pyramid of five pieces: a square 64, a square 49, a triangular 36, a triangular 25, and a round 16. So they looked sort of like this:

The Kings are generally treated specially: in most variants, they have enhanced powers of movement, and capturing the opponent's King is at least part of the objective of the game. Usually, the King can be captured intact or piecemeal, capturing its component pieces out of the pyramid. The details vary from version to version, however.

Play

Since each variant is a bit different, I will only speak in broad generalities here. Roughly speaking, movement happens by turns, as in most board games; each player gets to make one move on his turn. The three shapes move differently; in general, the squares move furthest and the rounds move least. Movement is never affected by the number on a piece -- the numbers are relevant mainly for capture.

While each version has a couple of degenerate captures (eg, surrounding a piece completely), capture is generally done mathematically. The details of this vary greatly, but in general you capture opposing pieces by creating mathematical relationships between those pieces and your own. For example, if two of your men are positioned by an enemy man, and they add up to his value, they capture him. Note that capture frequently does not require actually jumping into the enemy's space, as Chess does; you can often capture simply by setting the position up.

In most versions, captured men can then be subverted; when you capture the man, you flip him over (so that your color shows), and re-enter him on your side. This is essential in some cases, since most numbers exist only on one side or the other.

Victory

There are many, many different ways that a Rhythmomachy game can be won, from very simple "basic" victories to the Great Victories. The latter involve capturing the enemy king, then using your men to form mathematical sequences in enemy territory. Which victories were allowed varies from version to version, but I would generally recommend some practice just getting the basics before trying to win one of the advanced forms.

Appendix: Mathematical Proportions

There are many different kinds of mathematical relationships that can figure in Rhythmomachy. I assume that the reader is capable of dealing with basic arithmetic: addition, subtraction, multiplication, and division. These will serve you fine in most of the basics of the game. But for the more advanced versions of the game, and for the higher victories, you need to understand the three major forms of Proportions: Arithmetic, Geometric, and Harmonic. Don't worry about learning these upfront; they can come later. Also, all of the proportions available in the game are available as tables in Fulke, the period source from which I took these reconstructions. It is common to look up the proportions in tables, especially at first.

In general, all of these proportions are ways of defining a relationship between three numbers. In all of these examples, I will talk about three numbers A, B, and C, where A is the smallest number and C the largest. I will give examples for each, as well.

Arithmetic Proportion

Three numbers are in arithmetic proportion when the difference between A and B is the same as the difference between B and C. For example, the numbers 2, 4, and 6 form an arithmetic proportion, because (4 - 2) = (6 - 4). Similarly, 5, 25, and 45 form an arithmetic proportion, because (25 - 5) = (45 - 25).

In other words, the numbers are rising in a simple progression, adding the same number each time. 5 plus 20 is 25; 25 plus 20 is 45; so 5, 25, and 45 form an arithmetic proportion. Another way to think of it is that there is a number X, such that (A + X) = B, and (B + X) = C.

There are 49 arithmetic proportions available among the numbers in Rhythmomachy, according to Fulke.

Geometric Proportion

This is similar to arithmetic proportion, except that instead of adding the same number to go from A to B and B to C, you multiply instead. That is, the ratio between A and B is the same as the ratio between B and C. Similar to the last concept above, there is a number X, such that (A x X) = B, and (B x X) = C.

So for example, 3, 12, and 72 are in geometric proportion, because (3 x 6) = 12, and (12 x 6) = 72. 2, 4, and 8 are in geometric proportion, because (2 x 2) = 4, and (4 x 2) = 8. A more sophisticated example would be 4, 6, and 9, which are in geometric proportion because (4 x 1.5) = 6, and (6 x 1.5) = 9. (Yes, this is a period example; they understood fractions perfectly fine.)

There are 27 geometric proportions available in Rhythmomachy, according to Fulke.

Harmonic Proportion

Harmonic, (or Musical in many period sources) proportion refers to the way that musical harmonies relate to each other. Mathematically, it is the relationship (C / A) = ((C - B) / (B - A)) -- the ratio between the largest and smallest numbers equals the ratio of the differences between both of those numbers and the middle one.

So for example, 3, 4, and 6 are in harmonic proportion, because (6 / 3) = 2, and ((6 - 4) / (4 - 3)) = 2 as well. Or 25, 45, and 225, because (225 / 25) = 9, and ((225 - 45) / (45 - 25)) = 9 also.

Personally, I find harmonic proportions incredibly hard to work out in my head, although I understand them mathematically. There are 17 harmonic proportions available in Rhythmomachy, according to Fulke.